Extra exercises#
Although the previous tutorials contained several exercises, it doesn’t hurt to practice some more! The following exercises will test your Python (and Pandas/Matplotlib) skills. Note that it does not contain any exercises on Numpy because this is not directly relevant to the Python/PsychoPy course.
Basic Python#
The following ToDos help you practice with basic Python syntax and operations.
ToDo: Add five to the value in the variable x below and then raise the result to the third power. Store the result in a variable named y.
Show code cell content
""" Implement the ToDo here. """
x = -3.5
### BEGIN SOLUTION
y = (x + 5) ** 3
### END SOLUTION
""" Tests the above ToDo. """
assert(y == 3.375)
print("Well done!")
Well done!
ToDo: From the list below (my_list), extract every element at an odd index (at index 1, at index 3, at index 5, etc.) and store it in a new variable named my_list_index_odd. Note: you don't have to use a for-loop for this (but you can, if you want). Remember: Python is zero-indexed (i.e., the first element is at index 0).
Show code cell content
""" Implement the ToDo here. """
my_list = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']
### BEGIN SOLUTION
my_list_index_odd = my_list[1::2]
### END SOLUTION
""" Tests the above ToDo. """
assert(my_list_index_odd == ['b', 'd', 'f', 'h'])
print("Well done!")
Well done!
ToDo: From the list below (my_list2), extract the strings with five or more letters and store the result (another list) in a variable named my_list_filtered.
Show code cell content
""" Implement the ToDo here. """
my_list2 = ['hello', 'dear', 'student', ',', 'good', 'luck', 'on', 'this', 'ToDo!']
### BEGIN SOLUTION
my_list_filtered = [s for s in my_list2 if len(s) > 4]
# or:
my_list_filtered = []
for s in my_list2:
if len(s) > 4:
my_list_filtered.append(s)
### END SOLUTION
my_list_filtered
['hello', 'student', 'ToDo!']
""" Tests the above ToDo. """
assert(my_list_filtered == ['hello', 'student', 'ToDo!'])
print("Well done!")
Well done!
ToDo: From the list below (my_list3, extract all even numbers (e.g., 0, 2, 100, 52) and store the result (another list) in a variable named my_list_even. Note: this ToDo is testing your google skills!
Show code cell content
""" Implement the ToDo here. """
my_list3 = [1, 8, -4, 0, 5820, 6823591, 99, 87, 27, 2386, 1242, 1111, 582353]
### BEGIN SOLUTION
my_list_even = [v for v in my_list3 if v % 2 == 0]
# or:
my_list_even = []
for v in my_list3:
if v % 2 == 0:
my_list_even.append(v)
### END SOLUTION
""" Tests the above ToDo. """
assert(sorted(my_list_even) == [-4, 0, 8, 1242, 2386, 5820])
print("Well done!")
Well done!
ToDo: The list below (graded_per_day) contains integers that represent the number of essays I graded in the past week (Monday-Friday). Compute the percentage of essays I graded for each day and store the result (another list) in a new variable with the name percentage_per_day. Hint: to get a percetage, you divide a number by the sum of the collection and then multiply it by 100.
Show code cell content
""" Implement the ToDo here. """
graded_per_day = [20, 10, 8, 12]
### BEGIN SOLUTION
percentage_per_day = [v / sum(graded_per_day) * 100 for v in graded_per_day]
### END SOLUTION
""" Tests the above ToDo. """
assert([float(p) for p in percentage_per_day] == [40.0, 20.0, 16.0, 24.0])
print("Well done!")
Well done!
ToDo (difficult!): The covariance between two variables ($x$, $y$) of length $n$ is computed as follows:
(7)#\[\begin{align}
\mathrm{cov}_{xy} = \frac{\Sigma_{i}^{n} (x_{i} - \bar{x})(y_{i} - \bar{y})}{n-1}
\end{align}\]
Compute the covariance (a single float!) between the two lists (z1 and z2) below and store it in a variable with the name cov_z1z2. You may use the order of steps below:
Compute the mean of the two lists
Create two new lists in which each value has been subtracted with the list’s mean
Write a for-loop (or list comprehension) that multiplies each value in one list with the corresponding value in the other list (resulting in another list)
Sum the results from the previous step
Divide the result by the length of the list minus 1
Show code cell content
""" Implement the ToDo here. """
import random
z1 = [random.uniform(0, 1) for _ in range(20)]
z2 = [random.uniform(0, 1) for _ in range(20)]
### BEGIN SOLUTION
z1c = [v - (sum(z1) / len(z1)) for v in z1]
z2c = [v - (sum(z2) / len(z2)) for v in z2]
z1z2 = [z1c[i] * z2c[i] for i in range(len(z1c))]
cov_z1z2 = sum(z1z2) / (len(z1c) - 1)
### END SOLUTION
""" Tests the above ToDo. """
import numpy as np
assert(round(cov_z1z2, 3) == round(np.cov(z1, z2)[0, 1], 3))
print("Well done!")
Well done!
Matplotlib#
Two Matplotlib exercises (both relatively difficult).
ToDo: Below, we simulate the resting heart rate (rhr, in beats per minute) for 100 people, who are either male ('M') or female ('F') in this example (stored in the gend variable). Using Matplotlib, plot the histogram of the resting heart rate of males and females separately, but in the same plot! Make sure that the transparency of the bars of the histograms are set to 50% (google this!). Add a legend and sensible axis labels.
Show code cell content
""" Implement the ToDo here. """
np.random.seed(42)
rhr = np.random.normal(62, 4, size=500).astype(int).tolist()
gend = [np.random.choice(['M', 'F']) for _ in range(500)]
### BEGIN SOLUTION
import matplotlib.pyplot as plt
for g in ['M', 'F']:
data = [rhr[i] for i in range(100) if gend[i] == g]
plt.hist(data, alpha=0.5)
plt.legend(['M', 'F'])
plt.xticks([45, 50, 55, 60, 65, 70, 75, 80])
plt.ylabel('Frequency')
plt.xlabel('Resting heart rate')
#plt.savefig('rhr_by_gender.png')
plt.show()
### END SOLUTION
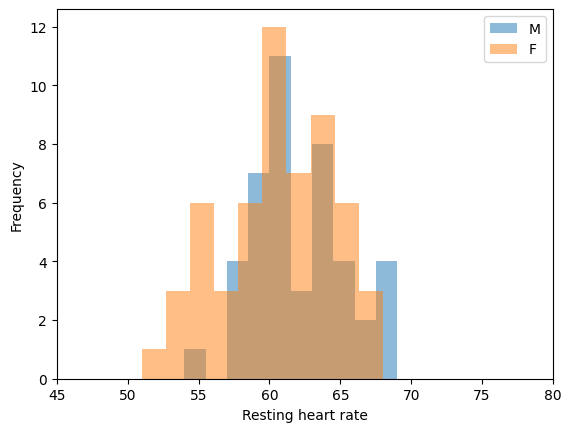
""" Tests the above ToDo. """
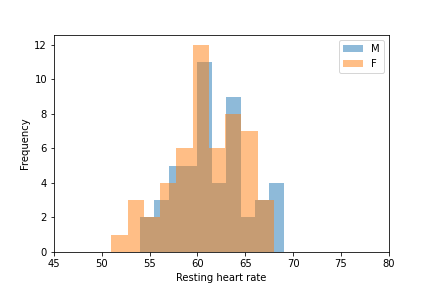
# Your plot should look like the one below!
from IPython.display import Image
Image('rhr_by_gender.png')
ToDo: Create a bar graph with the average heart rate for three groups:
- People with a RHR < 58 ("athletic")
- People with a 58 ≤ RHR ≤ 65("average")
- People with a RHR > 65 ("sedentary")
Do this separately for men (“M”) and women (“F”), such that there are six bars (athletic/men, athletic/women, average/men, average/women, sedentary/men, sedentary/women).
Show code cell content
""" Implement the ToDo here. Requires quite a lot of code! """
### BEGIN SOLUTION
avs = []
for g in ['M', 'F']:
dat = [rhr[i] for i in range(len(rhr)) if gend[i] == g]
dat_ath = [val for val in dat if val < 58]
avs.append(sum(dat_ath) / len(dat_ath))
dat_ave = [val for val in dat if val >= 58 or val <= 65]
avs.append(sum(dat_ave) / len(dat_ave))
dat_sed = [val for val in dat if val > 65]
avs.append(sum(dat_sed) / len(dat_sed))
labels = ['Athletic (M)', 'Average (M)', 'Sedentary (M)',
'Athletic (F)', 'Average (F)', 'Sedentary (F)',
]
plt.bar(labels, avs)
plt.xticks(labels, rotation=90)
plt.ylabel('Resting heart rate (b.p.m.)')
plt.show()
### END SOLUTION
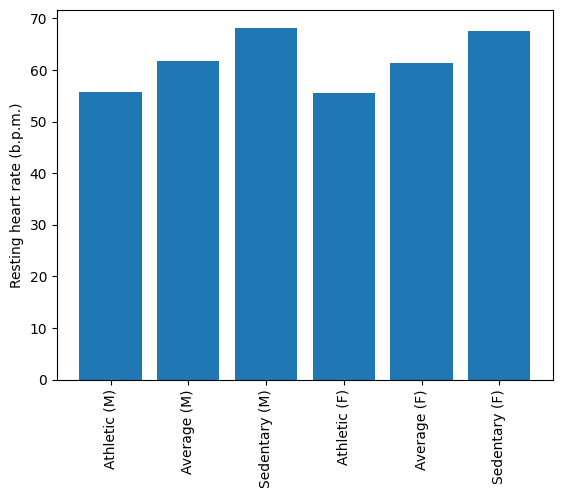
""" Tests the above ToDo. """
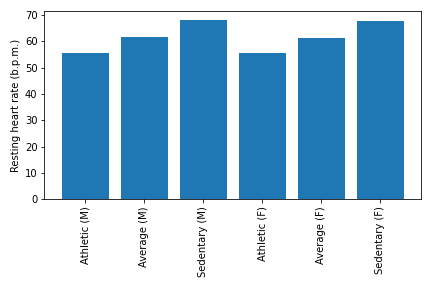
# Your plot should look like the one below!
from IPython.display import Image
Image('rhr_stratified.png')
Pandas#
Some Pandas exercises.
import random
import pandas as pd
n = 30
df = pd.DataFrame({
'participant_id': ['sub-' + str(i).zfill(2) for i in range(1, n + 1)],
'gender': [random.choice(['M', 'F']) for _ in range(n)],
'condition': ['A', 'B', 'C'] * (n // 3),
'prop_correct': np.random.uniform(0.4, 1, size=n),
'mean_rt': np.random.normal(200, 20, n)
})
df.iloc[np.random.choice(range(n), size=2), -1] = np.nan
ToDo: Remove all participants with missing reaction time data ("mean_rt" column) and store it in a new variable named df_clean.
Show code cell content
""" Implement the ToDo here. """
### BEGIN SOLUTION
df_clean = df.dropna(axis=0)
### END SOLUTION
""" Tests the above ToDo. """
assert(df_clean.shape[0] == df.shape[0] - 2)
assert(df_clean.shape[1] == df.shape[1])
print("Well done.")
Well done.
Let’s delete the original df for now:
del df
ToDo: Select from the df_clean dataframe the subset of male participants and save them in a new dataframe with the name df_m.
Show code cell content
""" Implement the ToDo here. """
### BEGIN SOLUTION
idx = df_clean.loc[:, 'gender'] == 'M'
df_m = df_clean.loc[idx, :]
### END SOLUTION
""" Tests the above ToDo. """
assert(all(df_m.loc[:, 'gender'] == 'M'))
print("Well done!")
Well done!
ToDo: Select from the df_clean dataframe the subset of participants who have more than 65% correct ("prop_correct") and a mean reaction time smaller than 100 ms. Store the result in a new variable named df_select.
Show code cell content
""" Implement the ToDo here. """
### BEGIN SOLUTION
idx = (df_clean.loc[:, 'prop_correct'] > 0.65) & (df_clean.loc[:, 'mean_rt'] < 200)
df_select = df_clean.loc[idx, :]
### END SOLUTION
""" Tests the above ToDo. """
assert(all(df_select.loc[:, 'mean_rt'] < 200))
assert(all(df_select.loc[:, 'prop_correct'] > 0.65))
print("Well done!")
Well done!
ToDo: Add a new column to the dataframe, "status", which contains either the string "above_average" or "below_average" depending on whether the participant has a "prop_correct" score higher than the average or lower than the average, respectively. This column should be added to the df_clean dataframe. Note: if you get a "SettingWithCopyWarning", you may ignore this.
Show code cell content
""" Implement the ToDo here. """
### BEGIN SOLUTION
mu = df_clean.loc[:, 'prop_correct'].mean()
for idx in df_clean.index:
if df_clean.loc[idx, 'prop_correct'] > mu:
df_clean.loc[idx, 'status'] = 'above_average'
else:
df_clean.loc[idx, 'status'] = 'below_average'
### END SOLUTION
""" Tests the above ToDo. """
assert(all(df_clean.query("status == 'below_average'")['prop_correct'] < df_clean['prop_correct'].mean()))
assert(all(df_clean.query("status == 'above_average'")['prop_correct'] > df_clean['prop_correct'].mean()))
print("Well done!")
Well done!
ToDo: Using Matplotlib, create a scatterplot with the variables "prop_correct" (on the x-axis) and "mean_rt" (on the y-axis).
Show code cell content
""" Implement the ToDo here. """
### BEGIN SOLUTION
plt.scatter(df_clean.loc[:, 'prop_correct'], df_clean.loc[:, 'mean_rt'])
plt.xlabel('Proportion correct')
plt.ylabel('Mean RT')
plt.show()
### END SOLUTION
ToDo: Compute the correlation between proportion correct and mean RT (using, e.g., he pearsonr function from the scipy.stats module) for each group ("A", "B", and "C") separately. Store these three floats (i.e., the correlations) in a list with the variable name corrs_conditions. Hint: take a good look at what the pearsonr function returns exactly!
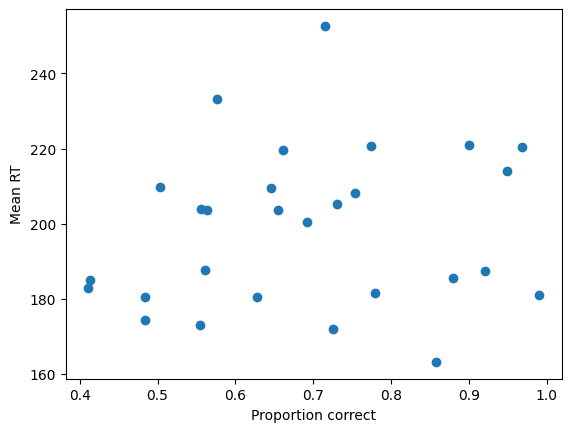
Note that, in real life, doing such “subgroup” analyses is probably a bad idea ;-)
Show code cell content
""" Implement the ToDo here. """
from scipy.stats import pearsonr
### BEGIN SOLUTION
corrs_conditions = []
for group in ['A', 'B', 'C']:
tmp = df_clean.loc[df_clean.loc[:, 'condition'] == group, :]
corr = pearsonr(tmp.loc[:, 'mean_rt'], tmp.loc[:, 'prop_correct'])[0]
corrs_conditions.append(corr)
### END SOLUTION
""" Tests the above ToDo. Don't use this implementation ;-)"""
ans = df_clean.groupby('condition')[['mean_rt', 'prop_correct']].corr().iloc[1::2, 0].tolist()
np.testing.assert_array_almost_equal(ans, corrs_conditions, decimal=4)
print("Well done!")
Well done!